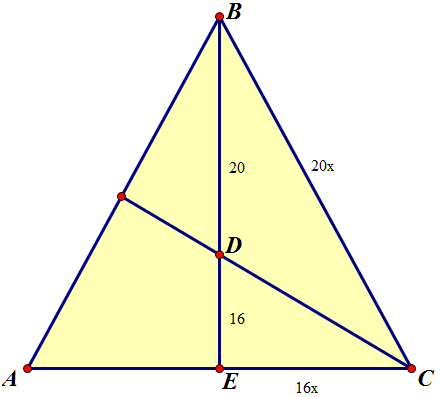
Рассмотрим треугольник ВСЕ (см. приложение). В нем биссектриса делит противолежащую сторону на два отрезка. Известно, что биссектриса делит сторону так, что отрезки пропорциональны прилежащим сторонам треугольника, поэтому ВС/ЕС=20/16. Значит, можно обозначить их длины как 20х и 16х соответственно.
Треугольник АВС равнобедренный, следовательно, его биссектриса ВЕ является также высотой и медианой. Из того, что она медиана, следует, что периметр Р=2ВС+2ЕС=72х, а из того, что высота - то, что к ВСЕ можно применить теорему Пифагора:

Мы уже знаем, что Р=72х. Подставляя, находим, что Р=216 см.