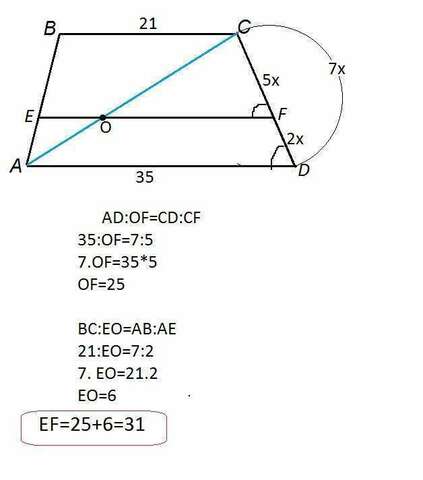
Сделаем рисунок.
Соединим А и С.
Точку пересечения АC и ЕF отметим О.
Треугольники АСD и OCF подобны по первому признаку подобия, т.к. углы при секущей СD и параллельных ЕF равны как соответственные.
Пусть коэффициент отношения отрезков СD и FD равен х.
Тогда СD=7х
АD:ОF=7:5
35:ОF=7:57=25
Аналогично углы при параллельных АD и ЕF и секущей АС равны.
Из подобия треугольников АВС и АЕО
ВС:ЕО=7:2
ЕО=6
ЕF=EO+OF=25+6=31