k є Z
второе( с вложением)
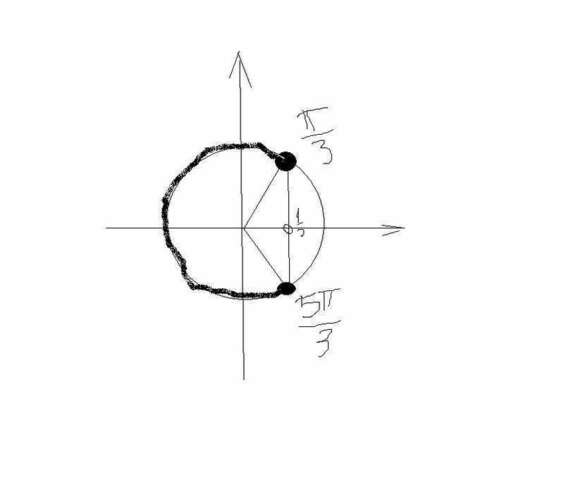
 \leq x \leq \frac{5\pi}{6}+\pi*k' alt='2cos(2x)-1 \leq 0;\\ cos (2x) \leq \frac{1}{2};\\ \frac{\pi}{3}+2*\pi*k \leq 2x \leq \frac{5\pi}{3}+2*\pi*k;\\ \frac{\pi}{6}+\pi*k \leq x \leq \frac{5\pi}{6}+\pi*k' align="absmiddle" class="latex-formula">
\leq x \leq \frac{5\pi}{6}+\pi*k' alt='2cos(2x)-1 \leq 0;\\ cos (2x) \leq \frac{1}{2};\\ \frac{\pi}{3}+2*\pi*k \leq 2x \leq \frac{5\pi}{3}+2*\pi*k;\\ \frac{\pi}{6}+\pi*k \leq x \leq \frac{5\pi}{6}+\pi*k' align="absmiddle" class="latex-formula">
x є [\frac{\pi}{6}+\pi*k;\frac{5\pi}{6}+\pi*k][/tex]
третье.
область определения
D(f)=R
Ищем производную
f'(x)=-3x^2+3x
Ищем критические точки

по свойствам квадратической функции
f'(x)>0 при (0;1)
f'(x)<0 при <img src="https://tex.z-dn.net/?f=%28-%5Cinfty%3B+0%29+%5Ccup+%281%3B%2B%5Cinfty%29" id="TexFormula7" title="(-\infty; 0) \cup (1;+\infty)" alt="(-\infty; 0) \cup (1;+\infty)" align="absmiddle" class="latex-formula">
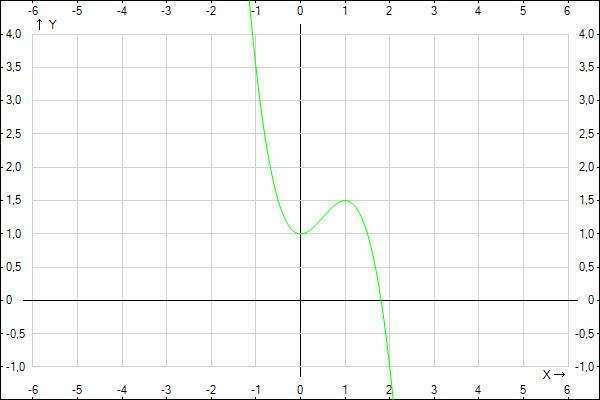
значит функция возростает на промежутке [0;1]
(см. вложение - из графика легко убедиться, что это действительно так)