Номер 565, 566, 571…………………………..

Question

Дан 1 ответ

Правильный ответ

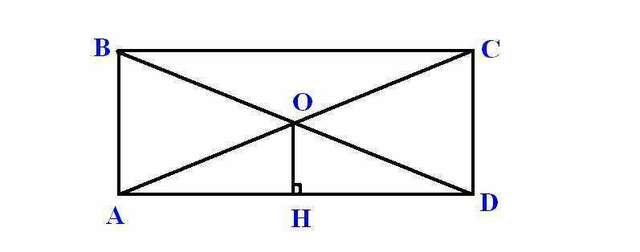
565) Треугольники АОН и АСD подобны по двум углам (А - общий, АНО=АDС). Учитывая, что диагонали прямоугольника точкой пересечения делятся пополам, получаем:
$\frac{AO}{OH} = \frac{AC}{CD} \\\ \frac{AO}{OH} = \frac{2AO}{CD} \\\ \frac{1}{OH} = \frac{2}{CD} \\\ CD=2OH \\\ CD=2\cdot2.5sm=5sm$
Ответ: 5 см

566) По условию следует, что отрезки АР и AQ вдвое меньше отрезков АВ и АС. Так как P и Q - середины сторон, то PQ является средней линией треугольника, которая в два раза меньше стороны ВС. Значит, каждая сторона треугольника АРQ в два раза меньше соответствующих сторон треугольника АВС, следовательно периметр треугольника АВС в два раза больше периметра треугольника APQ.
$P_{ABA}=2P_{APQ}=2\cdot21sm=42sm$
Ответ: 42 см

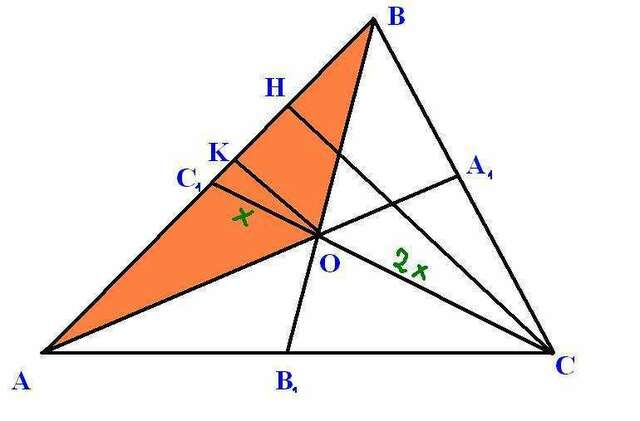
571) Проведем третью медиану СС₁, а также высоты СН и ОК.
$S_{ABC}= \frac{1}{2} AB\cdot CH \\\ S_{ABO}= \frac{1}{2} AB\cdot OK \\\ \frac{S_{ABC}}{S_{ABO}} = \frac{CH}{OK}$
Треугольники СНС₁ и ОКС₁ подобны по двум углам (С₁ - общий, С₁КО=С₁НС=90°), значит:
$\frac{CH}{OK} = \frac{CC_1}{OC_1} \Rightarrow \frac{S_{ABC}}{S_{ABO}} = \frac{CC_1}{OC_1}$
Так как медианы точкой пересечения делятся в отношении 2:1 считая от вершины, то:
$\frac{S_{ABC}}{S_{ABO}} = \frac{CC_1}{OC_1}= \frac{CO+OC_1}{OC_1}=\frac{2x+x}{x}=3 \\\ S_{ABC}=3S_{ABO}=3S$
Ответ: 3S

Artem112_zn (270k баллов) 30 Март, 18