Tg (π+x)=√3
tg x=√3
x=arctg√3+πn, n ∈ Z
x=π/3 +πn, n ∈ Z
2ctg(2π+x)-tg(π/2+x)=√3
2ctgx+ctgx=√3
3ctgx=√3
ctgx=√3/3
x=π/3+πn, n ∈ Z
-√3tg(π-x)=1
√3tgx=1
tgx=1/√3
x=π/6+πn, n ∈ Z
ctg(2π-x)+tg(3π/2 + x)=2
-ctgx-ctgx=2
-2ctg=2
ctgx=-1
x=3π/4 + πn, n ∈ Z
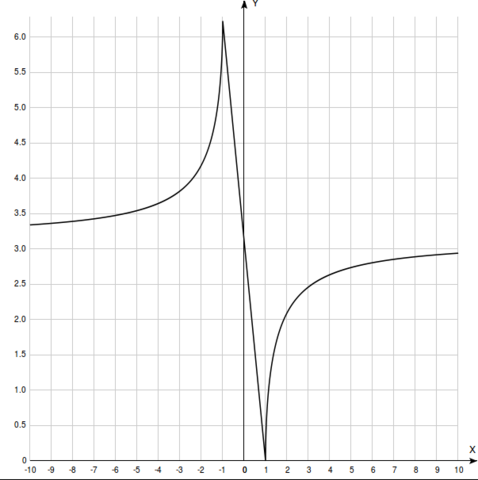
ГрАфик под Б смотреть во вложении
y=arccos(1/x)+arccos(-1/x)=arccos(1/x)+arccos(1/x)=2arccos(1/x)