1)Тут такая штука. Центр описанной окружности - это середина гипотенузы. Из этой середины опустить перпендикуляр на известный катет и получится Δ, в котором один катет = 2,5, другой = 6, а гипотенузу (R) надо искать . По т. Пифагора R² = 6² + 2,5² = 36 + 6,25 = 42,25 ⇒ R = 6,5
r = 2. Решение во вложении.
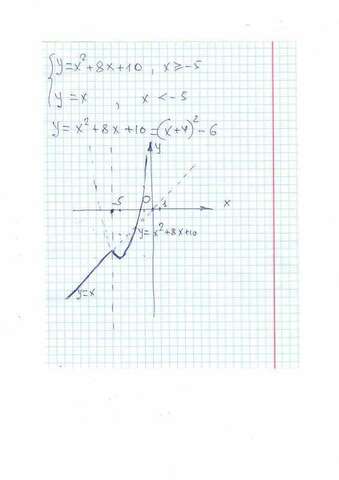
2) Чтобы построить график, надо понять: если бы не было записей х≥ -5 и х меньше 5, то на координатной плоскости появились бы парабола у = х² +8х + 10 и прямая у = х (это, кстати, биссектриса 1 и 3 четвертей)..
А ограничения говорят о том, что на одной части координатной плоскости кусок параболы, а на другой- кусок биссектрисы.