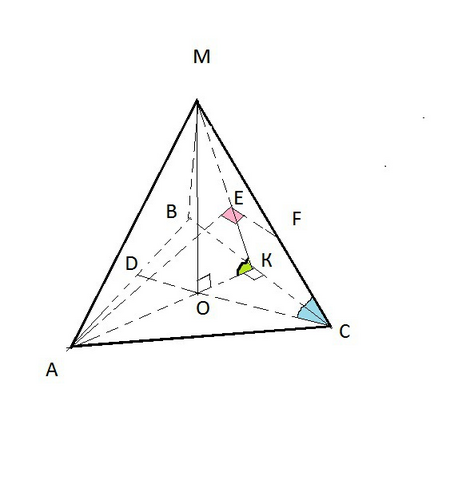
Cм. рисунок в приложении
В основании пирамиды равносторонний треугольник АВС:
АВ=ВС=АС=4 см.
В равностороннем треугольнике все высоты равны.
Высоты являются одновременно медианами и биссектрисами.
МО ⊥ пл. АВС.
ОА=ОВ=ОС=R ( радиус описанной окружности).
R=a√3/3, где а- сторона правильного треугольника.
ОА=ОВ=ОС=4√3/3
ОК=OD=r ( радиус вписанной окружности).
Медианты в точке пересечения делятся в отношении 2:1, считая от вершины.
r=R/2=2√3/3
Равные проекции имеют равные наклонные.
МА=МВ=МС.
а) АК- высота, медиана и биссектриса Δ АВС.
АК⊥ВС
ВК=КС.
МК⊥BC по теореме о трех перпендикулярах ( проеция МК- ОК, ОК⊥ВС, так как АК ⊥ ВС).
ВС ⊥ АК и ВС⊥ МК
ВС ⊥ двум пересекающимся прямым плоскости АМК, значит по признаку перпендикулярности прямой и плоскости, ВС ⊥ пл. АМК, а значит и пл. АМО.
Чтобы найти линейный угол двугранного угла между плоскостями АМО (АМК) и ВМС, надо провести перпендикуляры к линии их пересечения.
Линией пересечения является МК.
Проводим АЕ⊥МК и ЕF║ВС. (ВС⊥МК ⇒ ЕF⊥MK).
б) Угол между плоскостями АВС и МВС.
Линией пересечения плоскостей является сторона ВС.
АК⊥ВС
МК⊥ВС
Угол МКА - линейный угол двугранного угла.
Из прямоугольного треугольника МОК
tg ∠МКО=MO/OК=2/(2√3/3)=√3
∠МКО=60°
в) угол между прямой МС и плоскостью АВС - угол между прямой и её проекцией на эту плоскость.
Проекцией МС на плоскость АВС является ОС.
Из прямоугольного треугольника МОС
tg∠MCO=MO/OC=2/(4√3/3)=√3/2
∠MCO=arctg (√3/2).