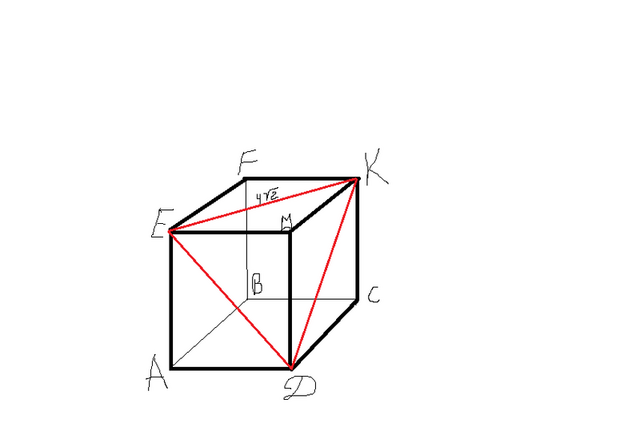
Правильная четырехугольная призма - это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники.
Sбок = 16 дм²
ЕК = 4√2
Sсечения ЕДК = ?
ΔЕМК прямоугольный равнобедренный
ЕК² = ЕМ² + МК² ЕМ = МК = а
ЕК = √(2а²)
4√2 = √(2а²)
4√2 = а√2
а = 4
ЕМ = МК = 4 дм
Sбок = ЕМ × МД
16 = 4 × МД
МД =4 дм
Значит боковые ребра призмы, как и основания, имеют форму квадрата
Значит все диагонали будут равны.
ЕК = ЕД =КД отсюда следует, что
Δ ЕКД равносторонний
S ЕКД = (√3)/4 × ЕК² = (√3)/4 × (4√2)² = (√3)/4 ×32 = 8√3 дм²