РЕБЯТКИ ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА КРОМЕ 4 И 6 ЗАДАНИЙ

Question

Дан 1 ответ

Правильный ответ

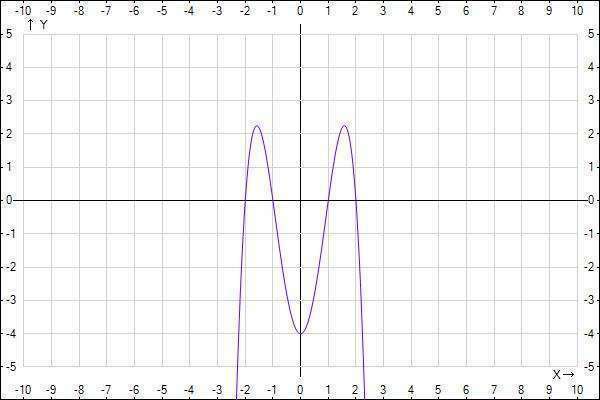
1/ Исследовать функцию и построить график

$y=-x^4+5x^2-4=-(x^2-1)(x^2-4)=-(x-1)(x+1)(x-2)(x+2);$

Область определения: область действительных чисел, так как функция - многочлен 4-й степени без ограничений на х,

$D(y)=R=(-\infty; \infty);$

Область значений:

Периодичность: непериодична как многочлен

Четность: функция четная (ООФ симметричина относительно точки х=0)

$y(-x)=-(-x)^4+5(-x)^2-4=-x^4+5x^2-4=y(x)$

Точки пересечения с осью Ох(y=0):

-(x-1)(x+1)(x-2)(x+2)=0;

(1;0); (-1;0); (-2;0); (2;0)

Точки пересечения с осью Оy(x=0)

y=-0^4+5*0^2-4=-4;

(0;-4)

Точки экстремума

$y'=-4x^3+10x;\\ y'=0;\\ -4x^3+10x=0;\\ 2x(x^2-5)=0;\\ x_1=0; x_2=\sqrt{5}; x_3=-\sqrt{5};$

+[-корень(5)] - [0] + [корень(5)] -

значит точка x=0 - точка минимуму

точки x=^+_-\sqrt{5}" alt="x=^+_-\sqrt{5}" align="absmiddle" class="latex-formula"> - точки максимума

Промежутки возростания $(-\infty;-\sqrt{5}) \cup (0;\sqrt{5})$

Промежутки убывания $(-\sqrt{5};0) \cup (\sqrt{5}; +\infty)$

Точки перегиб $y''=-12x^2+10;\\ y''=0;\\ -12x^2+10=0;\\ -2(6x^2-5)=0;\\ x_1=-\frac{5}{6}; x_2=\frac{5}{6}$

-[-корень(5/6)] +[корень(5/6)] -

значит функция выпукла на $-\frac{5}{6};\frac{5}{6}$

вогнута на $(-\infty;-\frac{5}{6}) \cup (\frac{5}{6}; +\infty)$

Асимптоты: не имеет, как многочлен

график во вложении.

$\int{3x^5+\frac{3}{x^3}+\sqrt[4] x+3}\, dx=\\ \int{3x^5}\, dx+\int \frac{3}{x^3}}\, dx+\int{\sqrt[4] x}\, dx+\int{3}\, dx=\\ 3\int{x^5}\, dx+3\int x^{-3}\, dx+\int{x^{\frac{1}{4}}}\, dx+\int{3}\, dx=\\ \frac{3x^6}{6}-\frac{3}{2x^2}+\frac{4}{3 \sqrt[4] {x^3}}+3x+C$

$\int {sin x+\frac{1}{cos^2 x} }\, dx=\\ \int {sin x}\, dx+\int {\frac{1}{cos^2 x} }\, dx=\\ -cos x+tg x+C$

$\int\limits^1_8 \sqrt[3] x-\frac{2}{3}x} \, dx =\\ \frac{3}{4} x\sqrt[3] x-\frac{x^2}{3} | \limits^1_8 = \frac{3}{4} 8*\sqrt[3] 8-\frac{8^2}{3} -\frac{3}{4} 1*\sqrt[3]1-\frac{1^2}{3} =\\ 12-\frac{64}{3}-0.75-\frac{1}{3}=\frac{45}{4}-\frac{65}{3}=\frac{-125}{12}$

$x^2dy-(2xy+3y)dx=0; x_0=y_0=1;\\ x^2dy-y(2x+3)dx=0;\\ x^2dy=y(2x+3)dx;\\ \frac{(2x+3)dx}{x^2}=\frac{dy}{y};\\ \frac{d(x^2+3)}{x^2}=\frac{dy}{y};\\ ln |x^2+3|+c=|y|;\\ y=c(x^2+3);\\ 1=c(1^2+3);\\ c=0.25;\\ y=0.25(x^2+3)=0.25x^2+0.75$

$z=2(cos \frac{4\pi}{3}+i*sin \frac{4 \pi}{3})=\\ 2*(-cos \frac{\pi}{3}-i*sin \frac{\pi}{3})=\\ 2*(-\frac{1}{2}-i*\frac{\sqrt{3}}{2})=\\ -1-\sqrt{3}i$

Рассмотрим

1" alt="\lim_{n \to \infty}\frac{a_{n+1}}{a_n}=\\ \lim_{n \to \infty}\frac{\frac{3(n+1)^2}{2^{n+1}}}{\frac{3n^2}{2^n}}=\\ \lim_{n \to \infty} \frac{(n+1)^2 *2^n}{n^2*2*2^n}}=\\ \lim_{n \to \infty}2*(1+\frac{1}{n})^2=\\ 2*(1+0)^2=2>1" align="absmiddle" class="latex-formula">

за признаком Даламбера ряд расбегается

dtnth_zn (409k баллов) 27 Фев, 18