Площадь боковой поверхности конуса равна произведению его образующей на половину длины основания.
S=l π r
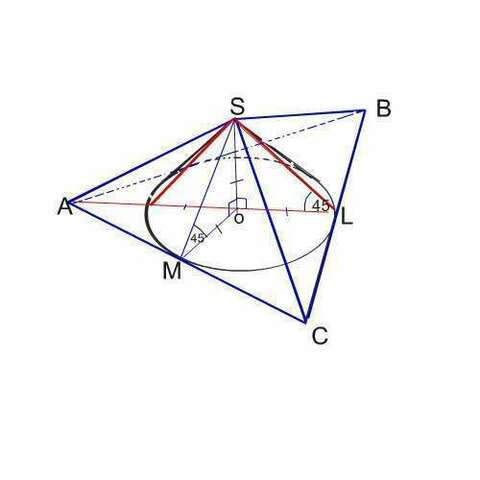
Нужно найти радиус OL конуса и его образующу SL
Основание конуса - вписанный круг.
Радиус вписанной окружности правильного треугольника, выраженный через его сторону r=(а√3):6
Образующую - апофему SL сторонвы СSB - найдем из равнобедренного прямоугольного треугольника SОL.
Как гипотенуза такого треугольника,
SL= ОL√2=r√2=(а√6):6
Площадь боковой поверхности конуса равна
S=l π r=(а√6):6)*(а√3):6)π= (а√6)(а√3)π:12=3aπ:12= 1/4 πa√2=(πa√2):4