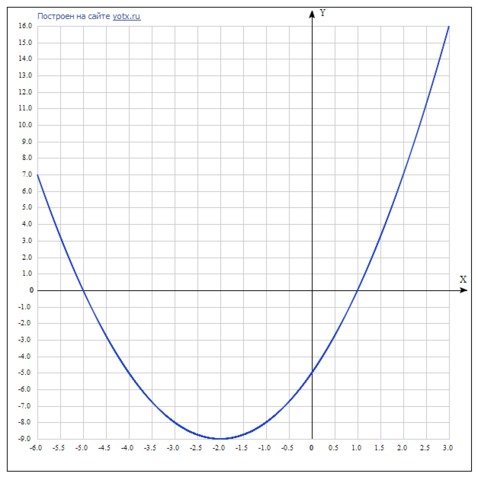
Координаты вершины параболы определяются по формуле:
Хо = -в / 2а = -4 / (2*1) = -2.
Уо = (-2)²+4*2-5 = 4+8-5 = 7 - подставляя значение Хо в уравнение параболы.
Пересечение с осями координат:
Ось ОУ пересекается при Х = 0. Подставляем х= 0 в уравнение:
У = -5.
Ось ОХ пересекается при У = 0. Приравниваем уравнение параболы нулю:
х²+4х-5 = 0 - получаем квадратное уравнение.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=4^2-4*1*(-5)=16-4*(-5)=16-(-4*5)=16-(-20)=16+20=36;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√36-4)/(2*1)=(6-4)/2=2/2=1;
x₂=(-√36-4)/(2*1)=(-6-4)/2=-10/2=-5.