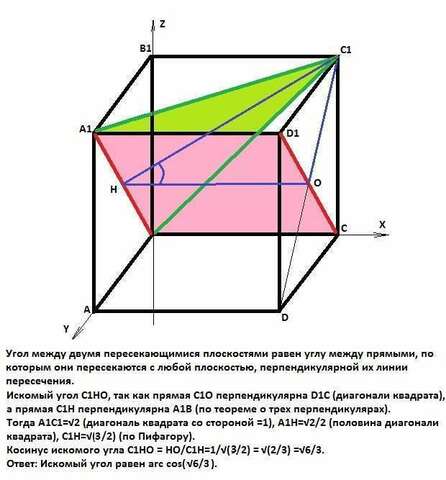
Двугранный угол между плоскостями равен линейному углу, образованному перпендикулярами к линии пересечения плоскостей (или, другими словами, сечением плоскостью, перпендикулярной к обоим плоскостям)
Искомый угол С1НО, так как прямая С1О перпендикулярна D1C (диагонали квадрата), а прямая С1Н перпендикулярна А1В (по теореме о трех перпендикулярах).
Тогда А1С1=√2 (диагональ квадрата со стороной =1), А1Н=√2/2 (половина диагонали квадрата), С1Н=√(√2/2)²+1) = √(3/2) (по Пифагору).
Косинус искомого угла С1НО = НО/С1Н=1/√(3/2) = √6/3.
Ответ: Искомый угол равен arc cos( √6/3).
Координатный метод:
Введем систему координат XYZ. Тогда
Даны точки: В(0;0;0) A1(0;1;1) C1(1;0;1) D1(1;1;1).
Составим уравнение плоскости ВА1С1 по трем точкам, используя формулу:
x-0 0-0 1-0 x-0 0 1
y-0 1-0 0-0 = 0. Или y-0 1 0 = 0.
z-0 1-0 1-0 z-0 1 1
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
1 0 0 1 0 1
(x-0)* 1 1 - (y-0)* 1 1 + (z-0)* 1 0 =0.
1*(x-0)-(-1)*(y-0)+(-1)*(z-0)=0
Получили уравнение плоскости ВА1С1: x+y-z=0
Составим уравнение плоскости ВА1D1 по трем точкам, используя формулу:
x-0 0-0 1-0 x-0 0 1
y-0 1-0 1-0 = 0. Или y-0 1 1 = 0.
z-0 1-0 1-0 z-0 1 1
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
1 1 0 1 0 1
(x-0)* 1 1 - (y-0)* 1 1 + (z-0)* 1 1 =0.
0*(x-0)-(-1)*(y-0)+(-1)*(z-0)=0
Получили уравнение плоскости ВА1D1: y-z=0
Если плоскость ВА1С1 задана общим уравнением x+y-z=0, то вектор n1{1;1;-1} является вектором нормали данной плоскости.
Если плоскость ВА1D1 задана общим уравнением y-z=0, то вектор n1{0;1;-1} является вектором нормали данной плоскости.
Угол между плоскостями можно найти через угол между нормальными векторами данных плоскостей по формуле:
cosα=(x1*x2+y1*y2+z1*z2)/[√(x1²+y1²+z1²) * √(x2²+y2²z2²)]
cosα=(0+1+1)/[√(1+1+1)*√(0+1+1)] или cosα=2/(√3*√2) = 2/√6 = √6/3.
Ответ: искомый угол равен arccos(2/√6) или arccos(√6/3).