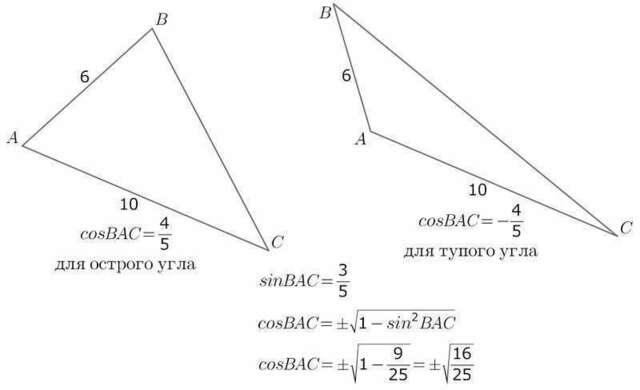
По т.косинусов можно определить вид треугольника, т.к.
косинус тупого угла -- число отрицательное,
косинус 90 градусов = 0
косинус острого угла -- число положительное)))
стороны треугольника 6 и 10 могут быть взаимно расположены так:
под острым углом друг к другу
или под тупым углом)))
они не перпендикулярны,
т.к. синус угла между ними не равен 1 по условию)))
синусы углов от 0 до 180 градусов -- числа положительные)))
отсюда два варианта...
основное тригонометрическое тождество позволяет определить косинус...
BC^2 = 100+36-2*60*cosBAC
BC^2 = 136-120*(4/5) = 136-96 = 40 или
BC^2 = 136-120*(-4/5) = 136+96 = 232
P = 16+2V10 или P = 16+2V58
S = 0.5*10*6*(3/5) = 30*3/5 = 18