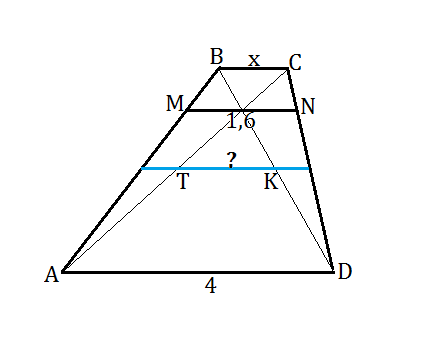
При решения задачи применим свойство трапеции, выведенное из подобия треугольников, образованных ее основаниями и диагоналями ( при желании доказательство можете найти в сети):
Отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции.
МN = 2ab/(a + b), где а- меньшее основание, b- большее.
ВС обозначим= а
1,6=2 а*4: (а+4)
1,6*(а+4)=8а
6,4=8а-1,6а
а=6,4:6,4=1
ВС=1
Другое свойство трапеции:
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
КЕ=(АД-ВС):2
КЕ=(4-1):2=1,5