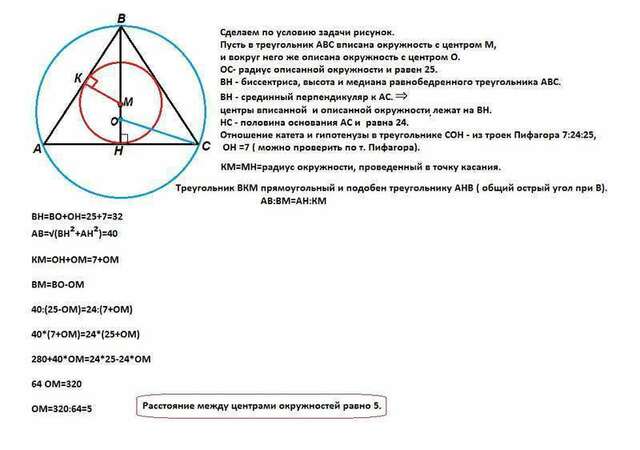
Сделаем рисунок, соразмерный данным в условии задачи размерам.
Пусть в треугольник АВС вписана окружность с центром М, и вокруг него же описана окружность с центром О.
ОС- радиус описанной окружности и равен 25.
ВН - биссектриса, высота и медиана треугольника АВС.
ВН - срединный перпендикуляр к АС.
Центр вписанной окружности лежит в точке пересечения биссектрис углов треугольника, центр описанной - на пересечении срединных перпендикуляров ⇒
центры вписанной и описанной окружности лежат на ВН.
НС - половина основания АС и равна 24.
Отношение катета и гипотенузы в треугольнике СОН - из троек Пифагора 7:24:25,
ОН =7 ( можно проверить по т. Пифагора).
МК - радиус окружности М, проведенный в точку касания. МК=МН
Треугольник ВКМ прямоугольный и подобен треугольнику АНВ ( общий острый угол при В).
АВ:ВМ=АН:КМ
ВН=ВО+ОН=25+7=32
АВ=√(ВН²+АН²)=40
КМ=ОН+ОМ=7+ОМ
ВМ=ВО-ОМ=25-ОМ
40:(25-ОМ)=24:(7+ОМ)
40*(7+ОМ)=24*(25+ОМ)
280+40*ОМ=24*25-24*ОМ
64 ОМ=320
ОМ=320:64=5
Расстояние между центрами вписанной и описанной окружностей треугольника равно 5