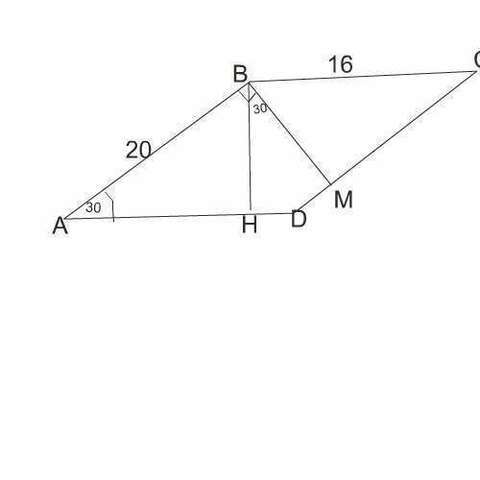
Сделаем рисунок
Так как высоота - отрезок, проведенный перпендикулярно стороне, в параллелограмме высота ВМ, проведенная к стороне DC, перпендикулярна так же и стороне АВ.
Поэтому угол АВМ - прямой, а угол АВН равен 90º-30º=60º
Следовательно, угол ВАН равен 30º
Известно, что в прямоугольном треугольнике катет, противолежащий углу 30º, равен половине гипотенузы.
Высота ВН=20:2=10 см
Площадь данного параллелограмма равна
S=AD*BH=16*10=160 см²