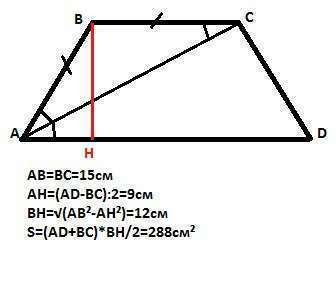
Равносторонняя трапеция АВСD.
Высота ВН равнобедренной трапеции, опущенная на большое основание, делит его на два отрезка, меньший из которых равен полуразности оснований.
Диагональ АС - биссектриса угла А, поэтому треугольник АВС равнобедренный, так как Итак, мы имеем прямоугольный треугольник АВН, в котором гипотенуза - сторона АВ=15, а катет АН=(33-15):2=9. тогда катет ВН (высота трапеции) равна по Пифагору √(15²-9²)=12см.
Площадь трапеции равна полусумме оснований, умноженной на высоту, то есть (15+33)*12/2 =288см²
Ответ: Sabcd=288 см²