Эта задача еще проще чем кажется :) и есть лишнее условие - длина стороны не понадобится (это понятно ДО решения - просто надо найти угол, который в правильной треугольной пирамиде образует грань с основанием, если задан угол между ребром и основанием, размеры пирамиды тут не причем).
Я сразу напишу решение, как оно возникает в голове :)
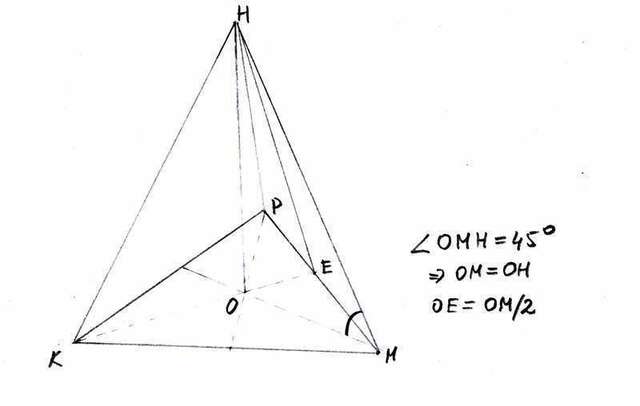
Правильная пирамида KPMH, KPM - основание, НО - высота. Проекция НМ на основание это ОМ, то есть радиус описанной окружности для треугольника КРМ. При этом ОН = ОМ, поскольку треугольник НОМ - прямоугольный с углом 45 градусов, то есть равнобедренный.
Пусть ОЕ перпендикуляр к РМ. Тогда МР перпендикулярно ОЕ и НО, и, следовательно, всей плоскости НОЕ, то есть НЕО - двугранный угол между плоскостями НРМ и КРМ.
С другой стороны, треугольник НОЕ - прямоугольный, и НО = ОМ = ОК = 2*ОЕ.
То есть тангенс искомого угла равен 2. (то есть угол НЕО = arctg2)
Это все.
Ясно, что угол между КМР и НКР такой же :)