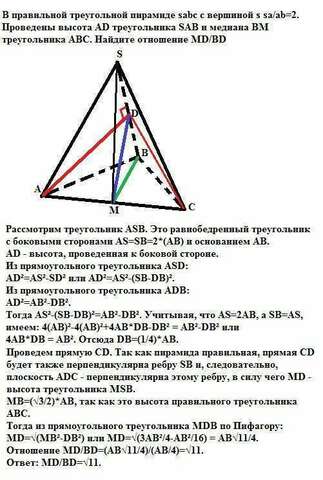
Рассмотрим треугольник АSВ. Это равнобедренный треугольник с боковыми сторонами AS=SB=2*(AB) и основанием АВ.
АD - высота, проведенная к боковой стороне.
Из прямоугольного треугольника АSD:
AD²=AS²-SD² или AD²=AS²-(SB-DB)².
Из прямоугольного треугольника АDB:
AD²=AB²-DB².
Тогда AS²-(SB-DB)²=AB²-DB². Учитывая, что AS=2AB, а SB=AS, имеем: 4(АВ)²-4(АВ)²+4АВ*DB-DB² = AB²-DB² или
4АВ*DB = AB². Отсюда DB=(1/4)*AB.
Проведем прямую СD. Так как пирамида правильная, прямая СD будет также перпендикулярна ребру SB и, следовательно, плоскость
АDC - перпендикулярна этому ребру, в силу чего
MD - высота треугольника МSВ.
МВ=(√3/2)*АВ, так как это высота правильного треугольника АВС.
Тогда из прямоугольного треугольника МDB по Пифагору:
MD=√(MB²-DB²) или MD=√(3AB²/4-AB²/16) = АВ√11/4.
Отношение MD/BD=(АВ√11/4)/(AB/4)=√11.
Ответ: MD/BD=√11.
P.S. MD можно найти и так: из прямоугольного треугольника ADB по Пифагору:
AD²=AB²-DB²=(15/16)AB². Из прямоугольного треугольника ADM (так как плоскость SMB перпендикулярна прямой АС) по Пифагору: MD²=АD²-АМ²=(15/16)AB²-(1/4)АВ²=(11/16)АВ². MD=АВ√11/4.