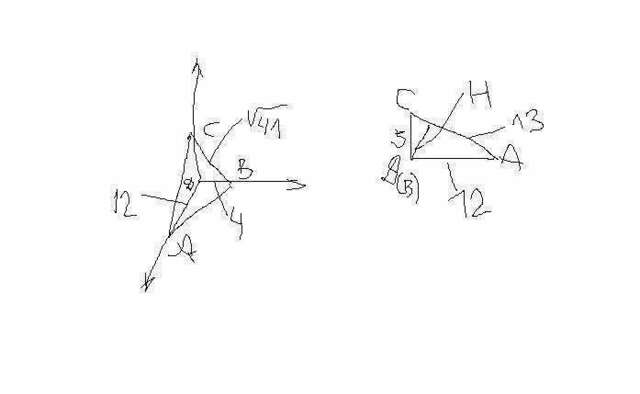
Если в треугольной пирамиде DABC все плоские углы при вершине D-прямые, то надо её перевернуть, чтобы основанием была грань DАВ. Тогда расстояние между прямыми AC и DB будет лежать в плоскости грани DСА как перпендикулярной к прямой DB.
DС =V(41 - 4^2) = V25 = 5
AC = V(12^2 + 5^2) = V(144 + 25) = V169 = 13.
Расстояние Н можно определить из площади треугольника DCA: S = 1/2*5*12 = 30
30 = 1/2*H*13 H = 60 / 13 = 4,615.