Решим аналогичную задачу, чтобы уметь решать любые подобные этой задачи:
*** ЗАДАЧА:
Сумма длин трех измерений прямоугольного параллелепипеда равна 60.
.
Найдите наибольшую из диагоналей граней параллелепипеда.
*** РЕШЕНИЕ:
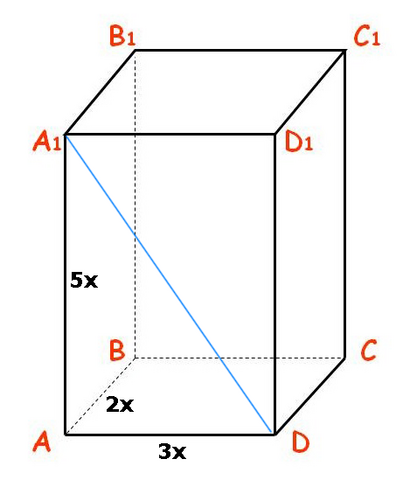
Все грани прямоугольного параллелепипеда – это прямоугольники (см рис)
Диагональ максимальна на грани, у которой максимальны стороны.
Значит нужно исключить самое короткое ребро, и взять грань, на которой нет этого ребра.
Учитывая пропорцию можно положить:
;
;
;
В условии сказано, что сумма всех трёх рёбер по разным направдениям равна 60, т.е.
;
;
;
x = 6 ;
Самое короткое ребро, понятное дело, это 
;
Берём грань без этого ребра, т.е. грань 
и расчитываем на ней диагональ по Теореме Пифагора;
Диагональ 
;
*** ОТВЕТ: 
;
В вашем случае все рассуждения аналогичны, ответ будет таким, что в квадрате он будет в 2 раза меньше тысячи.
