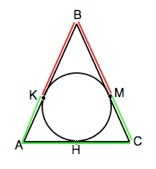
Обозначим треугольник АВС, АВ=ВС; точки касания К – на АВ, М –на ВС, Н – на АС.
Отрезки касательных к окружности, проведенных из одной точки, равны. ⇒
ВМ=ВК=4 (см)
СМ=СН=3 (см)
Так как треугольник равнобедренный и АВ=СВ, то
АК=СМ=3, и АН=АК=3
АВ=СВ=3+4=7 см, АС=АН+СН=3+3=6 см
Р=АВ+ВС+АС=20 см