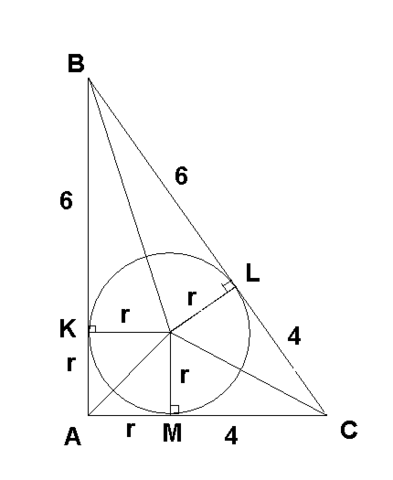
т.О - центр окружности вписаной в треугольник.
так как окружность касаеться сторон треугольника, то радиус этой окружности находиться под прямым углом к каждой стороне
получилось три пары треугольников: BKO и BLO; CLO и CMO; AMO и AKO - которые равны между собой как прямоугольные треугольники (за катетом - то наш радиус и гипотенузоэ - это общая сторона)
таким образом BK=Bl=6; CL=CM=4; AM=MO=AK=KO=r;
теперь основываясь на теореме пифагора
AB2+AC2=BC2
(r+6)2+(r+4)2=102
решаем квадратное уравнение и находим радиус
r=2 (второе решение уравнения отрицательное, а значит нам не подходит)
: