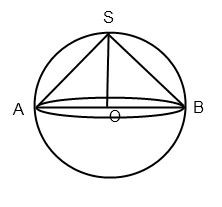
Основанием конуса будет большее сечение шара, так как радиус основания конуса равен радиусу шара по условию. Значит, высота конуса тоже равна радиусу шара.
Объем конуса находят по формуле:
V = ⅓ * π * R ² * h, где R - радиус основания, h - высота конуса.
Так как высота конуса равна радиусу шара формула примет вид:
V = ⅓ * π * R ³.
Объем шара: V = (4 * π * R ³) / 3. V = 36 ( по условию )
36 * 3 = 4 * π * R ³
108 = 4 * π * R ³
π * R ³ = 27.
Подставим значение π * R ³ в формулу объема конуса:
V = ⅓ * 27 = 9.