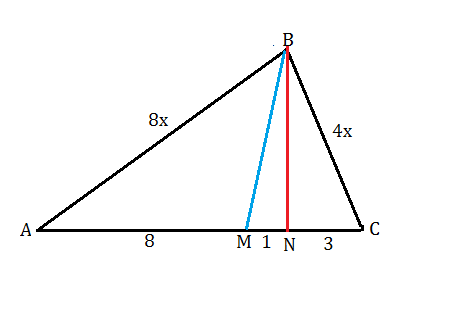
Сделаем риснок.
Биссектриса делит сторону, противолежащую углу, который делит, в отношении прилежащих к этому углу сторон.
Пусть коэффициент этого отношения будет х.
тогда АВ=8х,
ВС=НСх+МNх=4х
Выразим квадрат высоты ВN из прямоугольных треугольников, на которые она делит ∆ АВС.
Из Δ АВN
BN²=АВ²-AN²
Из ∆ BNC
BN²=BC²-NC² ; приравняем эти значения, т.к. они выражают одну и ту же величину.
AB²-AN²=BC²-NC²
АN=AM+MN=9
64х²-81=16х²-9
48х²=72
х²=1,5
Из ∆ ВNC
BN²=16*1,5-9=15
Ответ:BN²=15