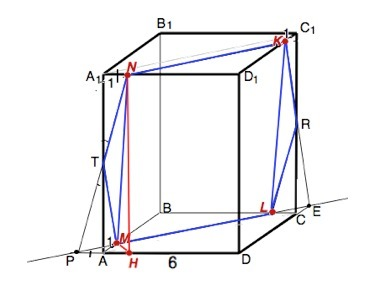
Плоскости оснований призмы параллельны. Следовательно, плоскость MNK пересекает их по параллельным прямым ( свойство), и МL параллельно NK.
ВМ=ND1=KD1=5. Треугольник ND1K равнобедренный, ⇒
NK=ND1:sin45°=5√2 ( или по т.Пифагора). Аналогично ML=5√2
а) Опустим из N перпендикуляр NH на АD.
AH=A1N=1, треугольник МАН равнобедренный – MH=√2.
NH=AA1=4√3 – из прямоугольного ∆ МНN гипотенуза
MN=(√(NH²+MH²)=√50=5√2 ⇒ MNKL - ромб.
Треугольник АМН равнобедренный, MBL- равнобедренный, ⇒ ML ║АС, МН ⊥ АС ⇒
HM⊥ML. По т. о 3-х перпендикулярах MN ⊥ML.
Аналогично КL перпендикулярна ML. ⇒
углы MNKL прямые, он - квадрат.
б) Продлим ML в обе стороны до пересечения с прямыми . DA и DC в точках Р и Е соответственно. Точки N и Р принадлежат плоскости АА1В1В, их можно соединить. Точки К и Е принадлежат плоскости DD1C1D, соединим их. Плоскость NPЕК пересечет АА1 в точке Т, а СС1 в точке R.
Соединим Т с N и М, R с К и L. Шестиугольник MTNKRL - сечение, площадь которого надо найти. Искомая площадь состоит из суммы площадей квадрата MNKL и площадей треугольников MTN и KRL.
Рассмотрим прямоугольный ∆ РАМ. Он подобен равнобедренному прямоугольнику МВL, следовательно, РА=АМ=1.
∆ ATP=∆ A1TN по катету и острому вертикальному углу при вершине Т. Следовательно, Т – середина АА1. AM=A1N, ⇒ ∆ АМT=∆ A1NT, откуда следует МТ=NT. Аналогично R – середина СС1, и KR=LR.
S ∆ PMN=S ∆ KLE = NM•PМ:2
Треугольник РАМ равнобедренный, след. РМ=АМ:sin45°=√2
S PMN=5√2•√2=5
Так как МТ - медиана, площадь треугольника MTN=5:2, а сумма площадей равных ∆ MTN и ∆ KRL равна 5
SMNKL=(5√2)²=50
S MTNKRL= 50+5=55 (ед площади).