Площадь боковой поверхности усеченного конуса 64см2 а площадь нижнего и верхнего...

Question 1

Площадь боковой поверхности усеченного конуса 64см2

а площадь нижнего и верхнего оснований соответственно 38п и 6п.Найдите угол между обрузующей и плоскостью основания этого усеченного конуса.

Question 2

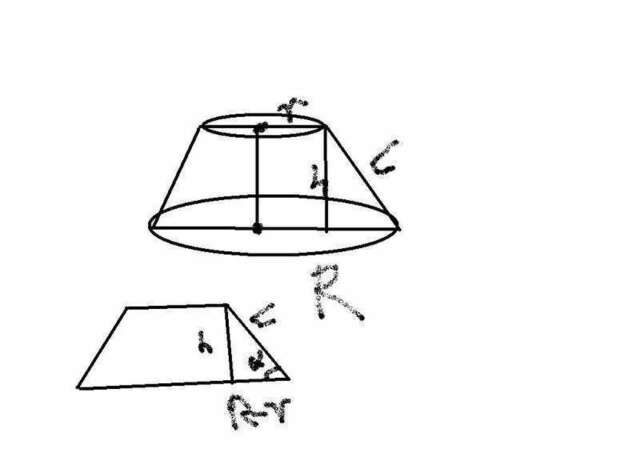
Радиус нижнего основания равен

$R=\sqrt{\frac{S_1}{\pi}}=\sqrt{\frac{38 *\pi}{\pi}}=\sqrt{38}$

Радиус верхнего основания равен

$r=\sqrt{\frac{S_2}{\pi}}=\sqrt{\frac{6 *\pi}{\pi}}=\sqrt{6}$

образующая усеченного конуса равна

$L=\frac{S}{\pi(R+r)}=\frac{64}{(\sqrt{38}+\sqrt{6})*\pi}=\\\\ \frac{64*(\sqrt{38}-\sqrt{6})}{(38-6)*\pi}}=\\\\ \frac{64*(\sqrt{38}-\sqrt{6})}{32*\pi}=\\\\ \frac{2*(\sqrt{38}-\sqrt{6})}{\pi}$

Высота по теореме Пифагора равна

$h=\sqrt{L^2-(R-r)^2}=\sqrt{(\frac{2*(\sqrt{38}-\sqrt{6})}{\pi})^2-(\sqrt{38}-\sqrt{6})^2}=(\sqrt{38}-\sqrt{6})*\sqrt{\frac{4-(\pi)^2}{(\pi)^2}$

Под корнем отрицательная величина, гдето в условии ошибка!!!

Дальше бы

Ищем угол между образующей и плоскостью основания этого усеченного конуса

$sin \alpha=\frac{h}{L}=$

а затем непосрественно угол

dtnth_zn · Answer 1 · 2018-03-10T10:43:08+0000