В равносторонний конус вписан шар найдите отношение площади полной поверхности конуса к...

$\frac{ S_{k} }{ S_{w} } = \frac{ \pi R_{k}( R_{k}+l ) }{4 \pi R_{w}^2 } = \frac{ R_{k}^2+R_{k}*l }{4 \pi R_{w}^2 }$ , где Sk - площадь полной поверхности конуса, Sw - площадь поверхности шара, Rk - радиус конуса, Rw - радиус шара, l = SB - образующая конуса.
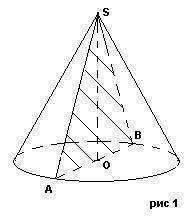
В равностороннем конусе осевым сечением является правильный (равносторонний) треугольник. AS = SB = AB = a (см рис). Значит, AB = a = 2Rk; а Rk = a/2, где a - сторона треугольника.
Радиус шара является радиусом вписанной в правильный треугольник окружности. Найдем этот радиус по формуле:
$R_{w} = \frac{a}{2 \sqrt{3} }$
Теперь подставим значение радиусов и найдем отношение:
$\frac{ S_{k} }{ S_{w} } = \frac{ R_{k}^2+R_{k}*l }{4 \pi R_{w}^2 }= \frac{ \frac{ a^{2} }{4} + \frac{ a^{2} }{2} }{4* \frac{a^2}{12} }= \frac{ \frac{3a^2}{4} }{ \frac{a^2}{3} }= \frac{9}{4}$
Ответ: 9/4.