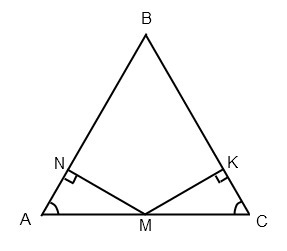
Построим равнобедренный ΔABC с основанием AC. На основании отметим точку M - середину AC. Проведем перпендикуляры к боковым сторонам MN и MK — это расстояния. Нужно доказать, что MN = MK.
∠NAM = ∠KCM (по свойству равнобедренного треугольника)/
∠ANM = ∠CKM = 90° (образованы перпендикулярами)
∠AMN = 90° - ∠NAM
∠CMK = 90° - ∠KCM
Значит ∠AMN = ∠KMC
AM = MC (M - середина AC)
ΔAMN = ΔCMK (по стороне и прилежащим к ней двум углам)
Значит MN = MK, что и требовалось доказать