6-8, очень нужно, спасибо огромное заранее)

A6.

$4^x=\frac{2^8*3^6}{6^6}=\frac{2^8*3^6}{2^6*3^6}=\frac{2^8:2^6}{2^6:2^6}=2^{8-6}=2^2=4\\x=1$

Ответ: цифра 1.

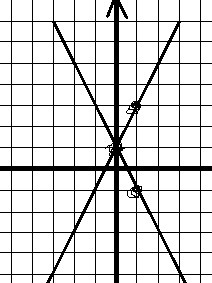
A7. (График во вложении)

$y=-2x+1\\x=0\to y=1;\\x=1\to y=-1$ – первая функция;
$y=2x+1\\x=0\to y=1;\\x=1\to y=3$ – вторая функция.

И без графика сказать можно, что точка пересечения – координата $(0;1)$ на плоскости, но график таки я вложу.

$(x_0;y_0)=(0;1)\to y_0-x_0=1-0=1$
Ответ: цифра 4.

A8.

Есть функция $y=kx+38$ , проходящая через точку $\alpha(15;-7)$ . Это значит, что значения икс и игрек, относящиеся к этой точки на плоскости, являются решением данного уравнения для $k$ (углового коэффициента, кстати). Подставляем, решаем и пишем ответ – всё просто.

$-7=k*15+38\\15k=-7-38=-45\to\\k=-3$
От себя могу добавить, что функция убывает, так как $k$ отрицательное.
Ответ: цифра 3.