Диагональ осевого сечения цилиндра 16 см и составляет с плоскостью основания угол 60...

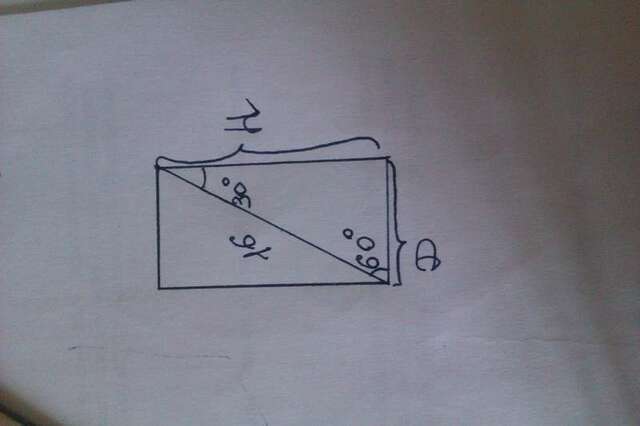
Т.к осевое сечение есть прямоугольник, а диагональ делит его на 2 прямоугольных треугольника.

Рассмотрим один из прямоугольных треугольников:

Диагональ составляет 60 градусов с диаметром основания, тогда диаметр равен 8, а радиус 4

Площадь полной поверхности есть:

2Sоснованая+Sбоковой поверхности= $2\pi*R^2+2\pi*R*H$

Где H-высота цилиндра находим ее из прямоугольного треугольника

получаем $8\sqrt3$

тогда площадь боковой поверхности равна:

$2\pi16+2\pi*4*8\sqrt3=32\pi (1+2\sqrt3)$

Рисунок рассматриваемого треугольника ниже