Радиус шара 15 см.
Вне шара дана точка А на расстоянии 10 см от его поверхности.
Найти
длину такой окружности на поверхности шара, все точки которой отстают от А на 20 см
Расстояние измеряется перпендикуляром. А находится на отрезке прямой, перпендикулярной диаметру искомой окружности.
Точка А от центра шара удалена на 15+10=25 см ( радиус + расстояние)
Все точки искомой окружности находятся на поверхности окружности основания воображаемого конуса, "надетого" на шар.
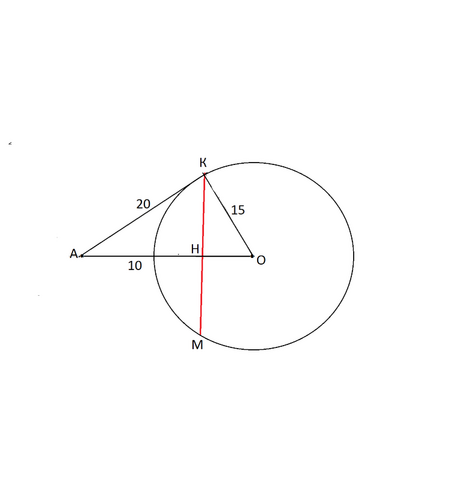
Смотрим схематический рисунок - разрез шара через центр и точку А.
АО=15+10=25 см.
ОК=R
АК - расстояние, на которое должна быть удалена точка А от поверхности.
КМ- диаметр искомой окружности,
КН - ее радиус.
Имеем треугольник АКО со сторонами, отношение которых 3:4:5 - отношение прямоугольного "египетского" треугольника.
Радиус искомой окружности КН - высота этого треугольика.
Чтобы найти высоту, применим свойство катета прямоугольного треугольника:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
Пусть отрезок гипотенузы, заключенный между катетом и высотой,
ОН =х
Тогда
ОК ²=х*25
25х=225
х=9
Из треугольника КНО
КН²=КО²-ОН²= 225-81=144
КН=r=12 см
Длина окружности с радиусом 12 см
С=2πr= 2π12=24π cм