1) Запишем это уравнение в виде (2x+5)(2y+3)=1 (проверяется раскрытием скобок и делением на 2).
Т.к. у 1 есть только два делителя 1 и -1, то возможны только 2 варианта: 2x+5=1, 2у+3=1, откуда х=-2, у=-1 или
2x+5=-1, 2у+3=-1, откуда х=-3, у=-2. Ответ: 2 решения.
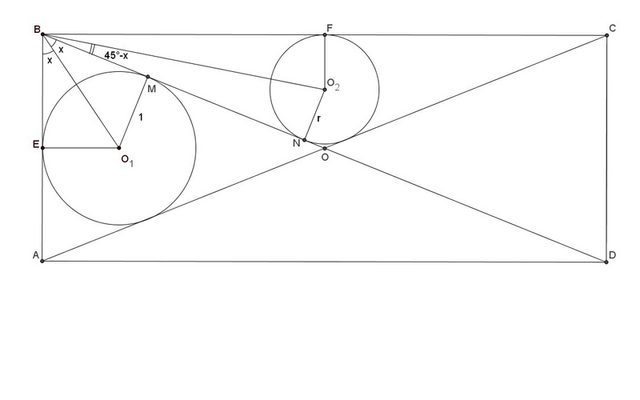
2) Введем обозначения как на рисунке. Пусть ∠O₁BM=x. BO₁ и BO₂ - биссектрисы углов, сумма которых равна 90°, поэтому ∠O₂BN=45°-x. По свойству касательных BE=BM=ctg(x) и BF=BN=r·ctg(45°-x), откуда BF/BE=r·ctg(45°-x)/ctg(x)=r·tg(x)/tg(45°-x). С другой стороны,
BF/BE=AD/AB=tg(2x). Таким образом, r·tg(x)/tg(45°-x)=tg(2x). После несложных преобразований получаем: r=2/(1+tg(x))². Т.к. х изменяется от 0 до 45°, то r может принимать значения от 1/2 до 2.