Человек стоит ** расстоянии 6 м от реки. ** расстоянии 34 м от реки горит костер....

Question

Человек стоит на расстоянии 6 м от реки. На расстоянии 34 м от реки горит костер. Расстояние между перпендикулярами, опущенными на берег реки из точек, в которых находятся человек и костер, равно 30 м. Человек бежит со скоростью 5 м/с к реке, зачерпывает ведро воды, потом бежит к костру и заливает его. Какое минимальное время необходимо для этого, если на зачерпывание воды уходит 5 с?

Answer 1

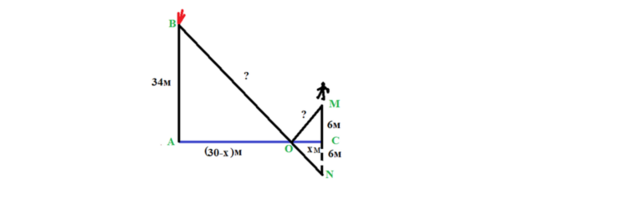
Зеркально отразим положение человека относительно берега реки, для этого продлим перпендикуляр от человека вниз за линию берега, отложим на нем отрезок СN=CM, и соединим точки N и В. Прямая NB - краткий путь к костру (теоретически). А практически - человек должен идти по берегу. Найдем этот путь.

СМ:АВ=СО:ОА

Пусть ОС - х м

АО - (30-х)м

6/34=х/(30-х) 

(30-х)6=34х

180-6х=34х

40х=180

х=4,5(м) - ОС

ОM=√6²+4,5²=7,5(м)

ВО=√34²+(30-4,5)²=42,5(м)

ВN=BO+OM=42,5+7,5=50(м) - краткий путь к костру

t=S:V

50:5=10(с) - время движения человека к воде, затем к костру 

5 с необходимо, чтобы зачерпнуть ведро воды 

10+5=15(с) - минимальное время, необходимое человеку, чтобы залить костер.

---