биссектриса острого угла параллелограмма делит его сторону ** отрезки длиной 6 см и 2...

Question

биссектриса острого угла параллелограмма делит его сторону на отрезки длиной 6 см и 2 см, считая от вершины тупого угла. Вычислите площадь параллелограмма, если его острый угол равен 30 градусов

Answer 1

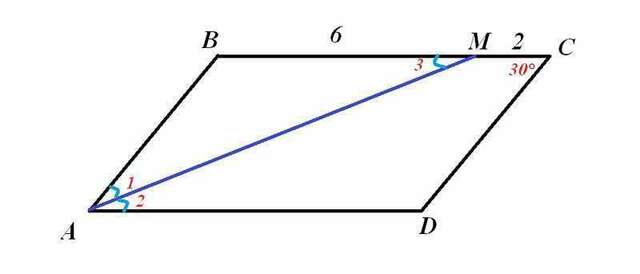
Чертеж во вложении.

Пусть АМ - биссектриса параллелограмма АВСД.

ВМ=6см, МС=2см.

Биссектриса делит острый угол А пополам, тогда ∠1=∠2.

Т.к. АД||ВС, АМ-секущая, то ∠2=∠3 (накрестлежащие)

Значит, ∆АВМ-равнобедренный с основанием АМ, тогда АВ=МВ=6см.

Значит, АД=ВС=ВМ+МС=6+2=8см.

Площадь параллелограмма S=BC*CD*sinC=8*6*0.5=24 см².

Ответ: 24 см².

 

---