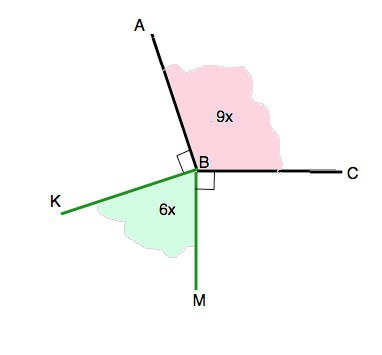
Пусть даны углы АВС и КВ`М.
Расположим их так, чтобы их вершины совпали. ( см.рисунок в приложении.
Так как по условию стороны этих углов взаимно перпендикулярны,
то КВ⊥АВ, а МВ⊥ВС.
Промежуточные углы КВА и МВС прямые.
Сумма всех четырех углов с общей вершиной равна 360°.
Тогда ∠АВС+∠КВМ=360°-(∠АВК+∠МВС)=180°
Примем коэффициент отношения данных углов равным х.
Тогда 6х+9х=180°, откуда х=12°
Угол АВС=9•12°=108º
Угол КВМ=6•12º=72°