окружности радиусов 13 и 20 пересекаются в двух точках, расстояние между которыми равно...

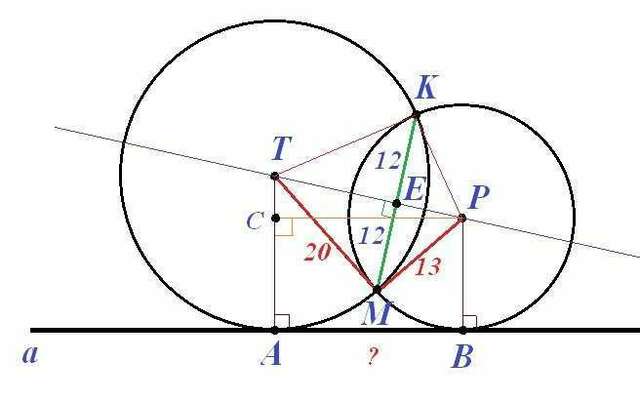
Чертеж к задаче - во вложении.
Пусть Т и Р - центры пересекающихся окружностей, К и М - точки пересечения окружностей. КМ = 24. А и В - точки касания окружностей с прямой а.
Радиусы ТА=ТМ=ТК=20, РВ=РМ=РК=13.
Согласно теореме: Окружность и прямая, а также две окружности могут пересечься не более чем в двух точках.При этом точки пересечения окружности с прямой симметричны относительно перпендикуляра к этой прямой, проходящего через центр, а точки пересечения двух окружностей симметричны относительно прямой, проходящей через их центры. - получим, что ЕМ=ЕК=12, ТР⊥КМ.
В ∆ ТМЕ по теореме Пифагора
$TE=\sqrt{TM^2-ME^2}=\sqrt{20^2-12^2}=\sqrt{400-144}=16$
В ∆ РМЕ по теореме Пифагора
$TE=\sqrt{PM^2-ME^2}=\sqrt{13^2-12^2}=\sqrt{169-144}=5$
Значит, ТР=ТЕ+ЕР=16+5=21.
Рассмотрим прямоугольную трапецию ТАВР. Проведем высоту РС.
Тогда АВ=РС, РВ=АС и ТС=ТА-АС=20-13=7
В ∆ ТРС по теореме Пифагора
$PC=\sqrt{TP^2-TC^2}=\sqrt{21^2-7^2}=\sqrt{441-49}=14\sqrt2=AB$
Ответ: $14\sqrt2$