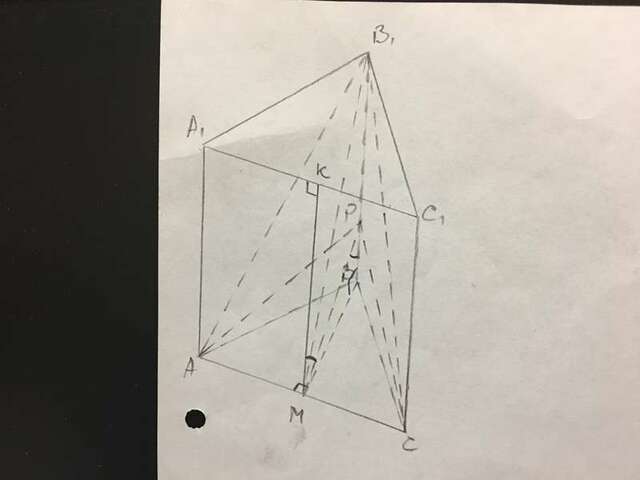
1) Прямоугольные треугольники АВР и СВР равны, т.к. АВ=ВС, и РВ - общая сторона, значит АР=СР, значит тр-ник АРС - равнобедренный.
Прямоугольные тр-ки АВВ1 и СВВ1 равны, т.к. АВ=ВС и ВВ1 - общая сторона, значит АВ1=СВ1 и тр-ник АВ1С - равнобедренный.
В равнобедренном треугольнике высота проведённая к основанию одновременно является медианой, значит АМ=СМ и основания высот РМ и В1М совпадают.
Доказано.
2) АМ=АС/2=16/2=8.
В тр-ке АВМ ВМ²=АВ²-АМ²=10²-8²=36,
ВМ=6.
РВ1=3РВ, значит РВ1:РВ=3:1=3х:1х ⇒ ВВ1=РВ1+РВ=4х,
4х=12,
х=3,
РВ=х=3.
В плоскости АСС1 восстановим перпендикуляр КМ к стороне АС.
КМ║АА1, АА1║ВВ1 ⇒ КМ║ВВ1, МР - их секущая, значит ∠KМР=∠MPB.
КМ∈АСС1, КМ⊥АС, РМ∈АРС, РМ⊥АС, значит нужно найти ∠КMP. Ищем угол MPB.
В тр-ке MPB tg(∠MPB)=BM/PB=6/3=2 - это ответ.