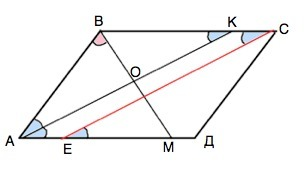
а) Сумма односторонних углов, образованных параллельными прямыми и секущей, равна 180°.
∠АВС+∠ВАД=180°.
Следовательно, сумма их половин
∠АВО+∠ВАО=(0,5∠АВС+0,5∠ВАД)= 180°:2=90°.
Из суммы углов треугольника ∠АОВ , образованный при пересечении биссектрис соседних углов параллелограмма, равен 180°-90°=90°.
б) Противоположные углы параллелограмма равны.
Равны и половины этих углов.
∠ВКА=∠ВСЕ.=∠СЕД=∠ВАК
Соответственные ∠ВКА и ∠ВСЕ при пересечении при АК║ЕС секущей ВС равны ⇒АК и СЕ -- параллельны. Аналогично доказывается параллельность или равенство биссектрис другой пары углов.
Если параллелограмм - ромб, то биссектрисы противоположных углов совпадают ( являются его диагоналями)