Высоты, проведённые из вершин меньшего основания равнобедренной трапеции, делят большее...

Question

Высоты, проведённые из вершин меньшего основания равнобедренной трапеции, делят большее основание на три отрезка, сумма длин двух из них равна длине третьего. Выполните рисунок и найдите площадь трапеции, если длина меньшего основания равна длине высоты и равна 6 см.

сделайте рисунок и напишите решение.

Answer 1

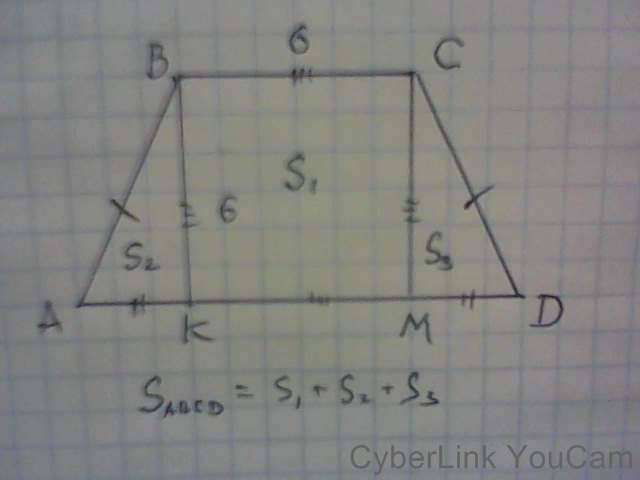
По условию: АВСD - трапеция, АВ=СD, ВК⊥АD, СМ⊥АD, ВК=ВС=СМ=КМ=6 см., ΔАВК=ΔDСМ.
АК+DМ=КМ, АК=DМ=х,
х+х=6, 2х=6, х=3 см.
ΔАВК. S(АВК)=0,5·ВК·АК=0,5·3·6=9 см², S2=S3=9 см².
S1=ВС·ВК=6·6=36 см².
S(АВСD)=S1+S2+S3=9+36+9=54 см².
Другой способ. ВС=6 см, АD=3+6+3=12 см. ВК=6 см ,
S(АВСD)= 0,5(ВС+АD)·ВК=0,5(6+12)·6=9·6=54 см².
Ответ: 54 см²

---