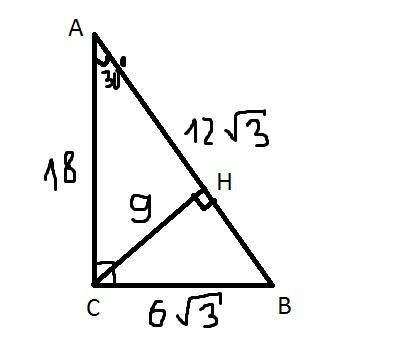
С=90°⇒треугольник прямоугольный.
По теореме, катет,лежащий против угла в 30° равен половине гипотенузы⇒
CB=12√3÷2=6√3
По теореме Пифагора
AB²=AC²+CB²
(12√3)²=x²+(6√3)²
432=x²+108
x²=432-108
x²=324
x=√324
x=18
Так как высота-это перпендикуляр,то ∠AHC-прямой⇒ΔAHC-прямоугольный.
∠A в ΔAHC= 30°.
По теореме,катет лежащий против угла в 30° равен половине гипотенузы⇒ CH=AC÷2
CH=18÷2=9
Ответ:9