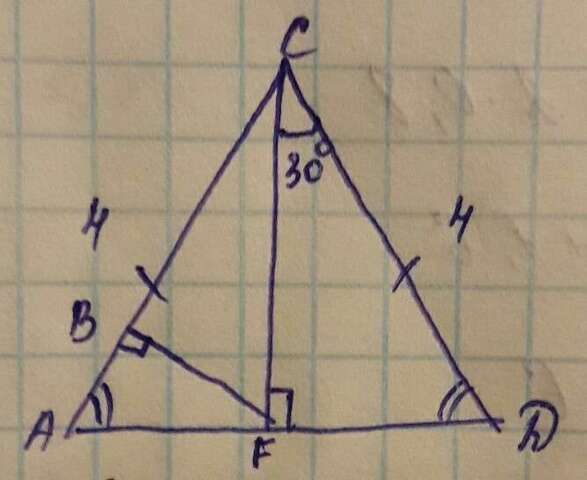
Угол FCD=углу FCA=30 градусов (CF- высота , медиана и биссектриса, тк треугольник АСD- равнобедренный).
AF=1/2AC (катет, лежащий против угла в 30 градусов , равен половине гипотенузы) . AF=1/2×4=2см.
угол А=углуD (углы при основании равны, тк треугольник ACD-равнобедренный)=(180-60)÷2=60 градусов.
угол AFB=180-(90+60)=30 градусов.
АВ=1/2АF (катет ,лежащий против угла в 30 градусов, равен половине гипотенузы) , АВ=1/2×2=1см.
ВС=АС-АВ ; ВС=4-1=3см.
Ответ: ВС=3 см.