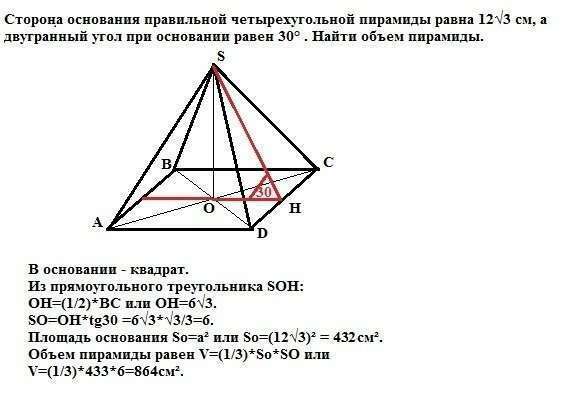
В основании правильной пирамиды - квадрат.
Вершина пирамиды проецируется в центр квадрата.
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. В нашем случае это угол SHO.
Из прямоугольного треугольника SOH:
ОН=(1/2)*ВС или ОН=6√3.
SO=OH*tg30 =6√3*√3/3=6 (так как tgα=SO/OH - отношение противолежащего катета к прилежащему.)
Площадь основания So=a² или So=(12√3)² = 432см².
Объем пирамиды равен V=(1/3)*So*SO или
V=(1/3)*433*6=864см².