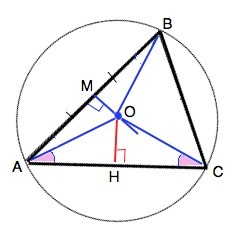
В ∆ АОС углы при основании АС равны. Следовательно, ∆ АОС –равнобедренный, и АО=ОС.
В ∆ АОВ отрезок ОМ⊥АВ и делит её пополам. ⇒
ОМ высота и медиана ∆ АОВ. ⇒ ∆ АОВ - равнобедренный, и
АО=ОВ. Отрезки АО=ОВ=ОС
Точки А, В и С находятся на одном и том же расстоянии от О, следовательно, принадлежат окружности, так как ей принадлежит множество точек плоскости, находящихся на одном и том же расстоянии от одной точки, ⇒
т.О - центр описанной около ∆ АВС окружности, ч.т.д.