Площадь трапеции равна произведению высоты на полусумму оснований ( т.е. на её среднюю линию).
В прямоугольной трапеции меньшей стороной является та, что составляет с основаниями прямой угол.
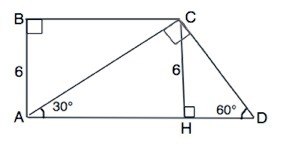
Обозначим трапецию АВСD.
АВ перпендикулярна основаниям, ∠СDA=60°, ∠САD=30°.
Опустим из вершины С высоту СН. Она отсекает от трапеции прямоугольный треугольник СНD.
HD=CH:tg60°=6/√3=2√3
АН=СН:tg30°=6√3
АD=AH+HD=8√3
BC=АН=6√3
 см²
см²