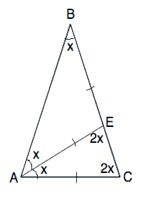
Биссектриса угла А делит треугольник на два равнобедренных. Найдите углы треугольника.
Обозначим треугольник АВС, биссектрису - АЕ, половину угла А=х
Тогда в ∆ АВЕ стороны АЕ=ВЕ, ∠ВАЕ=∠АВЕ=х
Так как АЕ - биссектриса, ∠ЕАС=∠ВАЕ=х
Сумма углов треугольника 180°.
В равнобедренном ∆ ЕАС углы при основании ЕС равны.
∠АЕС=∠АСЕ=(180°-х):2
Для ∆ АВС
∠А +∠В+∠С=180°
х+х+(180-х):2=180°
5х=180
х=36°
Отсюда ∠В=36°, углы А=С=2•36°=72°
--------
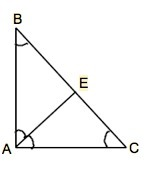
Нужно отметить, что в первую очередь думается о случае, когда биссектриса делит треугольник на два равных равнобедренных треугольника. .
В этом случае биссектриса будет одной из трёх равных сторон получившихся треугольников.
∆ АВЕ=∆ АСЕ, стороны ВЕ=АЕ=СЕ.
Получаем АЕ - медиана ∆ ВАС. Забудем на время, что если медиана равна половине стороны. к которой проведена, этот треугольник – прямоугольный.
В ∆ АВС угол А=угол В+С (из равенства половин угла А и углов В и С)
Пусть угол В=С=х
⇒∠А=2х
В ∆ ВАС угол А=2х, угол В=С=х, сумма 2х+х+х=180°
откуда х=45°.
Угол В=С=45°, угол А=90°