task/24715096
---.---.---.---.---.----
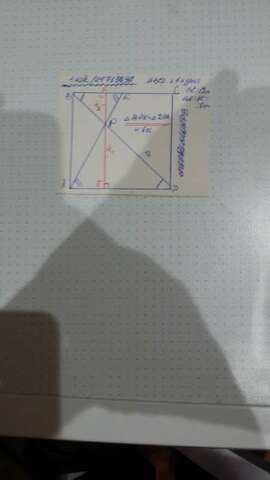
Квадрат имеет стороны 12. Середина стороны BC обозначена как K, а точка P - пересечения AK и BD. Найдите площадь треугольника BKP.
====================================================
рис прикреплен
S(BPK) =BK*PF/2 , но
BK =BC/2 =12/2 =6 ;
S(BPK) =6*PF/2 =
3*PF
остается найти высоту PF ( PF⊥ BC)
∆ BPK ~∆DPA (первый признак подобия )
∠PBK = ∠PDA
и
∠PKB = ∠PAD
как накрест лежащие углы
* * * еще ∠BPK = ∠DPA как вертикальные углы * * *
PF / PE = BK / DA ;
(высоты пропорциональны соответствующим сторонам_коэфф.подобия)
PF / PE =1/2 ⇒ PE=2BF с другой стороны PE+P
F = AD =12
2PF+PF =12 ; 3PF =12 ;
PF = 3.
Следовательно S(BPK) =3*3 = 9.
ответ : 9 кв. единиц .