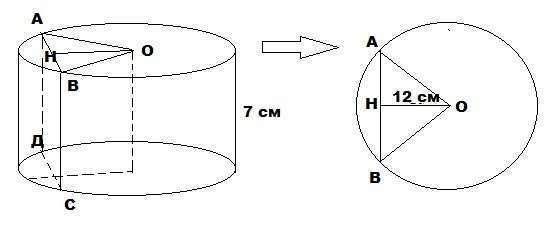
Построим цилиндр и проведем сечение (АВСД), удовлетворяющее
условиям задачи.
Данное сечение является прямоугольником со сторонами равными
высоте данного цилиндра (АД и ВС) и хорде, удаленной на 12 см от центра
основания (Центра окружности О) (АВ и ДС).
Найдем данную хорду:
АВ=70/7=10 см
Рассмотрим треугольник АОВ где АВ хорда данной окружности, АО и ВО радиусы, а ОН высота (расстояние от центра
окружности до хорды). Так как АО=ВО то высота будет являться и медианой – то
есть АН=АВ/2=10/2=5 см.
По теореме Пифагора найдем АО
АО=√(АН²+ОН²)=√(5²+12²)=√169=13 см.
Радиус цилиндра равен 13 см.