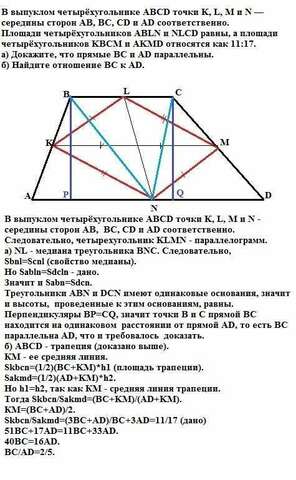
В выпуклом четырёхугольнике ABCD точки K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Следовательно, четырехугольник KLMN - параллелограмм (на всякий случай).
а) NL - медиана треугольника ВNC. Следовательно,
Sbnl=Scnl (свойство медианы).
Но Sabln=Sdcln - дано.
Значит и Sabn=Sdcn.
Треугольники АВN и DCN имеют одинаковые основания, (точка N - середина отрезка AD. Значит и высоты ВР и CQ, проведенные к этим основаниям, равны.
Перпендикуляры ВP=CQ, значит точки В и С прямой ВС находится на одинаковом расстоянии от прямой АD, то есть ВС параллельна AD,
что и требовалось доказать.
б) АВСD - трапеция (доказано выше).
КМ - ее средняя линия.
Skbcn=(1/2)(BC+KM)*h1 (площадь трапеции).
Sakmd=(1/2)(AD+KM)*h2.
Но h1=h2, так как КМ - средняя линия трапеции.
Тогда Skbcn/Sakmd=(BC+KM)/(AD+KM).
КМ=(ВС+АD)/2.
Skbcn/Sakmd=(3ВС+AD)/BC+3AD=11/17 (дано)
51ВС+17AD=11BC+33AD.
40BC=16AD.
ВC/AD=2/5.