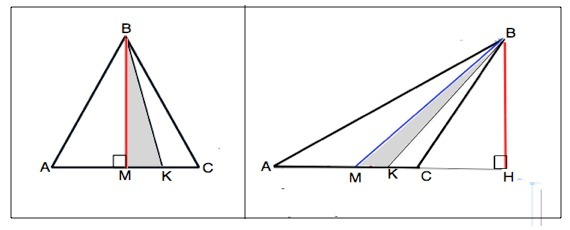
Отрезок ВМ – медиана равнобедренного треугольника АВС ( АВ=ВС), отрезок ВК – медиана треугольника ВМС (см. рисунок). Найдите площадь треугольника ВМК, если площадь треугольника АВС равна 48 см²
Медиана треугольника делит его на два равновеликих, т.е. равных по площади. ⇒ Ѕ АВМ=ЅВСМ=48:2=24 см²
Медиана ∆ ВМС также делит его на два равных по площади, ⇒ Ѕ ∆ ВМК=24:2=12 см²
-------
То, что ∆ АВС – равнобедренный, на результат решения не влияет (см. рисунок).
Площадь треугольника равна половине произведения высоты на сторону. к которой проведена.
Что в равнобедренном, что в другом треугольнике его площадь медианой делится пополам. Разница лишь в том, что медиана равнобедренного треугольника является и его высотой ( и биссектрисой).
Высота у ∆ АВМ и ВСМ общая, АМ=СМ, следовательно, их площади равны. Аналогично МК=КС, высота общая для треугольников ВМК и ВСК, – их площади равны площади ∆ АВС, дважды деленной пополам, то есть Ѕ/4.
S ∆ МВК=48:4=12 см²